North America - Welcome to "Timeout for Tech with Gary T. Fry, Ph.D., P.E."
 
Each month, we examine a technology topic about which professionals in the railway industry have asked to learn more.
 
This month our subject is wheel/rail contact and wheel load attenuation.
 
In North America, a steel wheel under a fully loaded rail car routinely supports 36,000 pounds of load.
 
As wheels roll over rails, the surfaces in direct contact flatten, much like pressing the tips of your fingers together.
 
This deformation results in the formation of a "contact patch" between the wheel and rail that is roughly the size of a U.S. dime, 0.4 square inches.
 
The average vertical pressure applied to the steel within the area of contact is roughly 90,000 PSI (pounds per square inch).
 
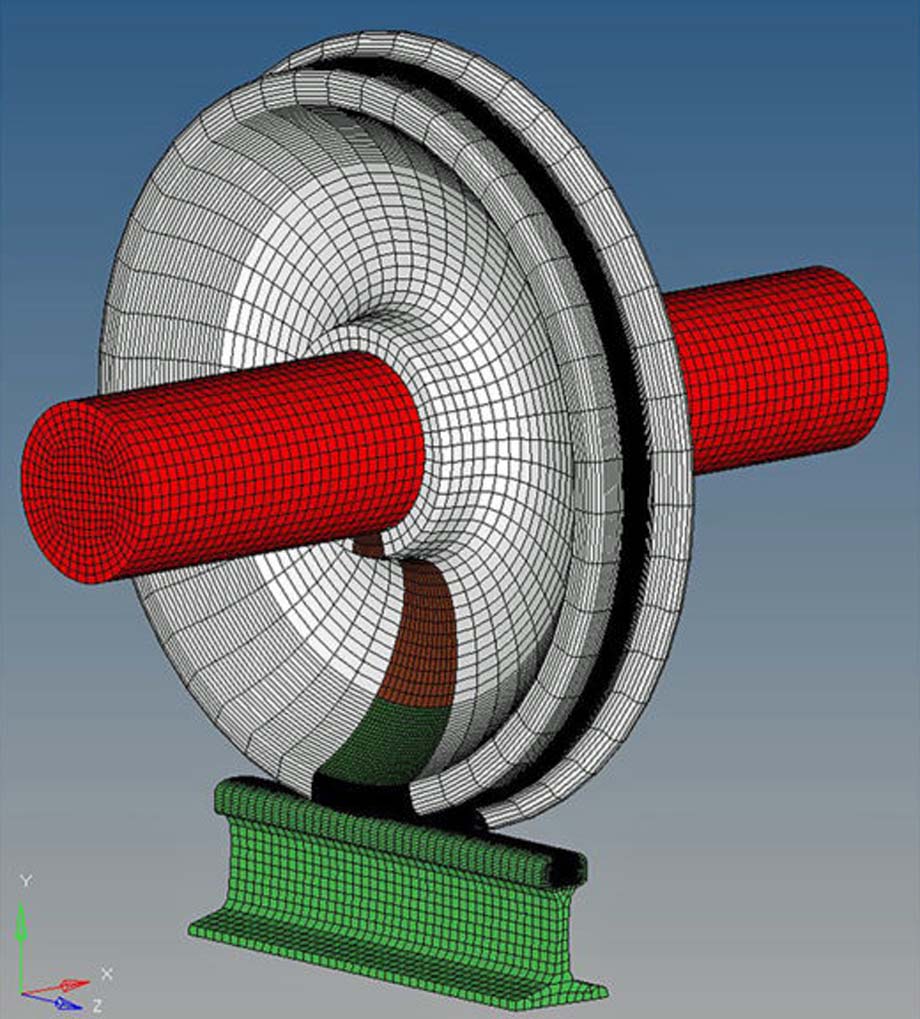
Figure 1 above shows a railway wheel in contact with a rail.
 
The very small contact patch under a heavy wheel load is one of the main reasons that trains are incredibly energy efficient.
 
The resulting pressure in this small contact patch, and its repeated application as wheels roll along the rails, present several interesting engineering challenges.
 
Before diving into those details, there are some other areas of contact visible in Figure 1 that we should consider: rail/tie-plate, tie-plate/tie, and tie/ballast.
 
To begin, we must recognize that the rail acts as a beam distributing each wheel load among a few ties.
 
When a wheel is directly over a tie, we can estimate simply that the load is shared among the five nearest ties such that a tie directly beneath the wheel receives 50 percent of the load.
 
As a result, the maximum force between each of the three contacting surfaces below the base of the rail at a given tie location is close to 18,000 pounds.
 
The notional area of contact between the base of the rail and a tie plate is roughly 45 square inches giving an estimated average vertical pressure of 400 PSI.
 
The notional area of contact between the tie plate and the timber tie is roughly 110 square inches, giving an estimated average vertical pressure of 170 PSI.
 
Finally, the notional area of contact between one half of a timber tie and the ballast is roughly 460 square inches, giving an estimated average vertical pressure of 40 PSI.
 
The important takeaway is this:
 
The average vertical pressure caused by a wheel load diminishes substantially at locations away from the immediate vicinity of the wheel/rail contact patch.
 
And that is an essential purpose of the track structure, to attenuate wheel loads so that heavy trains can be supported by the ballast and soil beneath.
 
Much more rigorous methods exist to model these pressures, but the takeaway is the same.
 
The average vertical wheel/rail contact pressure is roughly 2,000 times greater than the average vertical tie/ballast pressure.
 
Let's return to the wheel/rail interface.
 
Steel is used as the material of choice for wheels and rails.
 
Specifically, among other attributes, steel alloys are chosen that are economical to produce in large volumesm=, and are processed to be strong, resistant to forming fatigue defects, and resistant to abrasion and wear.
 
Especially over the past 40 years, the rail industry has made substantial progress in developing improved steel alloys and extending the safe lifespan of wheels and rails.
 
But fatigue cracks that form in wheels and rails remain a common root cause for component replacements and train accidents.
 
To help mitigate these undesirable outcomes and support development of improved materials, detailed computer models of wheel/rail contact can help our understanding of fatigue defects in wheels and rails.
 
Figure 2 below is a rendering of such a model.
 

Figure 2: Rendering of a detailed computational model of wheel/rail contact - Date? Gary T. Fry.

While not immediately apparent, this model includes a small, penny-shaped fatigue defect that the model predicted forming at a highly stressed location in the wheel rim.
 
Figure 3 below shows a close-up view of the location of the defect.
 

Figure 3: Close-up rendering of a small fatigue defect contained in a computational model of wheel/rail contact - Date? Gary T. Fry.

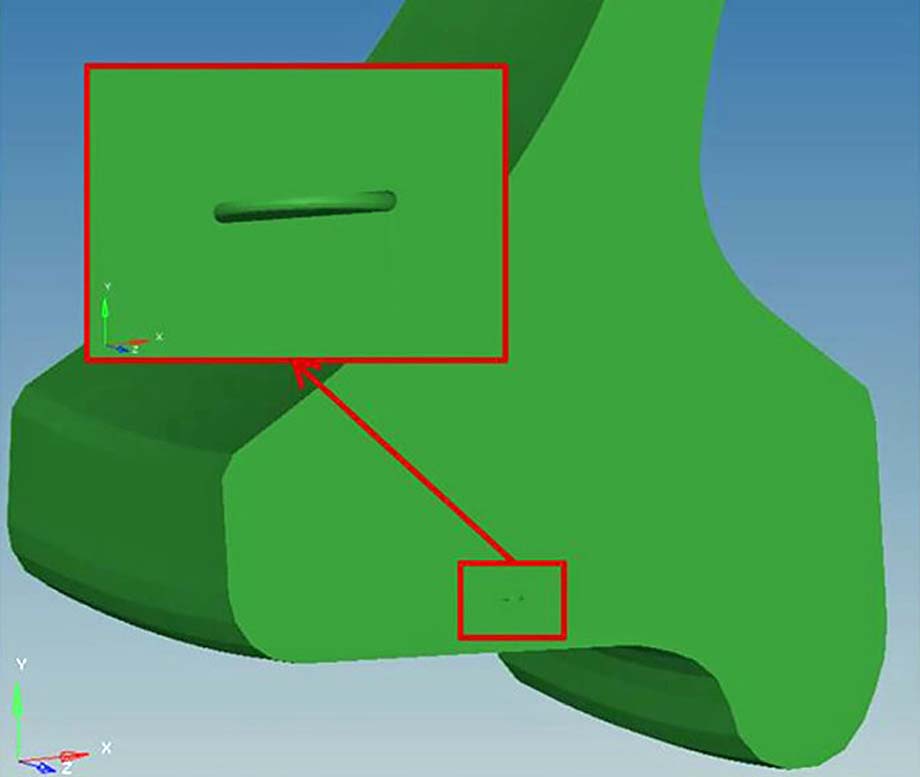
Figure 4 below shows a plot of the maximum stresses through a section of material surrounding the defect as the wheel rolls on the rail.
 

Figure 4: Plot of stresses in material surrounding a fatigue defect in a computational model of wheel/rail contact - Date? Gary T. Fry.

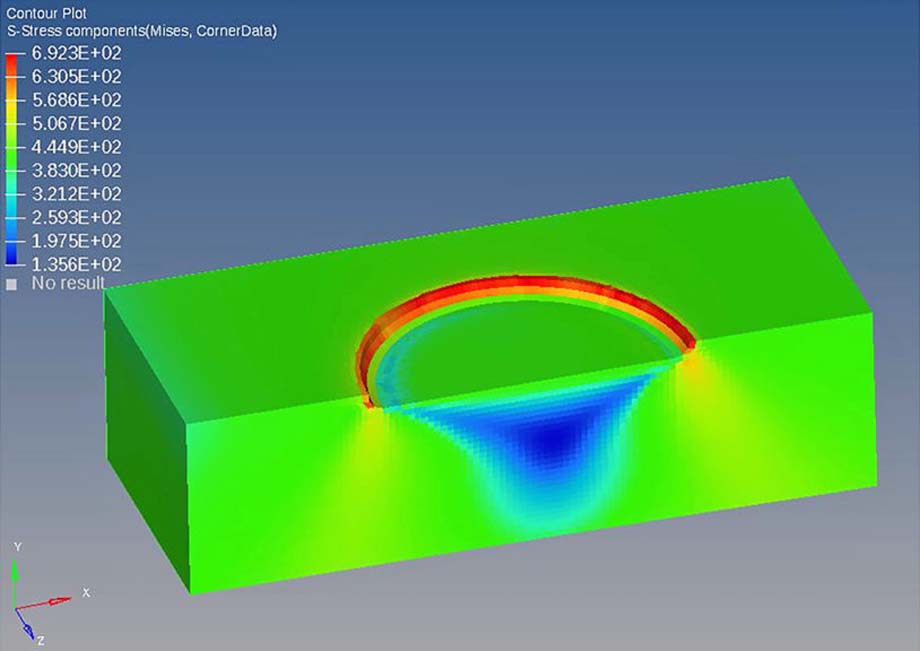
Computational models like these provide several insights.
 
We can use them to determine the most likely locations of fatigue defect formation, the most likely orientations of the defects, the growth rates of the defects, and the critical sizes of the defects that will result in component failure.
 
All that information is essential to designing inspection and maintenance programs that simultaneously mitigate the risk of component failure while optimizing component service life, utilization, and reliability.
 
These models can also help engineers design and evaluate new material systems and component details.
 
The goal is to identify essential characteristics that would represent improved performance for a material and/or component.
 
Then the behavior of the material/component is simulated under loading conditions representative of its expected use in service.
 
In the simulation environment, multiple candidate materials and components can be compared and ranked in terms of expected performance and are essentially prescreened as promising for further development and prototype testing.
 
Another role for computational modeling is designing and simulating the prototype testing.
 
Detailed models are becoming increasingly popular in this regard as a means of optimizing value and effectiveness of testing programs and associated data collection and processing.
 
So, what does the future promise in terms of improved materials and component designs for railway wheels, rails, tie-plates, and ties?
 
Two obvious objectives are increased defect-free service life and reduced maintenance under increased demands from trains.
 
That means developing materials with increased capacities against fatigue and other forms of degradation and developing components that offer reduced demand on their materials under load.
 
The future is bright if we continue to pursue the Five I's, Identify, Invest, Innovate, Implement, and Improve!
 
Gary T. Fry.